Fiche de révision probabilités
I – Vocabulaire des probabilités
- Expérience aléatoire : C’est une expérience qui a plusieurs résultats
possibles, mais dont on ne peut pas prévoir, ni calculer lequel va être réalisé. - Evénement : C’est une partie de tous les résultats possibles.
- Probabilité : Une probabilité représente les chances qu’un événement se produise lors d’une expérience aléatoire. Elle est comprise entre O et 1.
Exemple : Dans une urne on a 2 boules rouges, 3 boules vertes et 5 boules blanches de même taille et indiscernables au toucher.
L’expérience aléatoire : On tire au hasard une boule et on prend en compte sa couleur.
Soit A l’événement « la boule tirée est rouge », soit B l’événement « la boule tirée est verte »
Calcul des probabilités :
Il y a au total 10 boules, p(A) = 2/10 = 0, 2 et p(B) = 3/10 = 0,3
On va dire que l’on à 20 % de chance d’avoir une boule rouge et 30 % de chance d’avoir une boule verte.
- Evénement contraire : L’événement contraire de A, est l’événement qui se compose de tous les résultats de l’expérience aléatoire sauf ceux de A. Il est noté «
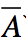» ou « non A ». On a p(non A) =1 – p(A)
Reprenons l’exemple précédent
L’événement A est « Ne pas obtenir une boule rouge », c’est à dire soit une boule verte, soit une boule blanche p(A) =1 – p(A) =1 – 0, 2 = 0,8
On a 80 % de chance de ne pas obtenir une boule rouge.
- Evénements incompatibles : Deux événements sont incompatibles si ils ne peuvent pas se réaliser en même temps.
Reprenons l’exemple précédent
A et B sont deux événements incompatibles, il est impossible d’obtenir en une boule, une boule qui soit à la fois rouge et à la fois verte.
II – Expérience aléatoire à deux épreuves
Une expérience aléatoire à deux épreuves serait par exemple lancer une pièce deux fois de suite.
Il est souvent très facile de représenter ces expériences sous forme d’un arbre de probabilités.
Exemple 1 : On lance une pièce deux fois de suite
Soit P l’événement « obtenir pile »
Ici la probabilité d’obtenir deux piles est 1/2 x 1/2 = 1/4 (On suit le chemin correspondant)
On a donc 25 % de chance d’obtenir deux piles de suite.
Exemple 2 :
Reprenons l’exemple avec les boules dans l’urne. Dans une urne on a 2 boules rouges, 3 boules vertes et 5 boules blanches de même taille et indiscernables au toucher On tire une boule puis on la remet, et on en tire une seconde, et on note les couleurs obtenues.
Soit R l’événement « la boule tirée est rouge »
Ici la probabilité d’obtenir deux boules rouges est
2/10 x 2/10 = 4/100 = 0, 04
On a suivi les branches correspondantes à l’événement R puis encore R
La probabilité d’obtenir une boule rouge et une boule d’une autre couleur est
2/ 10 x 8/10 + 8/10 x 2/10 = 32/100 = 0,32
Ici il y a deux chemins qui fonctionnent, on doit donc ajouter les résultats.
Remarque : la somme des probabilités de chaque nœud doit être égale à 1.
Partagez
