Exercice d’entraînement – Théorème de Pythagore
Un véliplanchiste très expérimenté fait une sortie en mer en jour de tempète où le vent atteint la vitesse de 100 km/h. À cette vitesse, la pression p du vent est estimée à 500 Pa.
Le but de l’exercice est de calculer la valeur exacte de la force exercée par le vent sur la toile dont le shéma est donné ci-dessous.
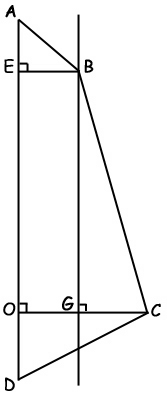
Partie 1 : Calcul de l’aire réelle de la voile
On donne AB=99 cm, DC = 200 cm, AE=70 cm, EO = 240 cm et OD = 120 cm.
1. Donner la nature des triangles ABE, CDO et BGC. Justifier les réponses.
Corrigé
2. a) Calculer en cm les longueurs de EB, OC. Arrondir le résultat à l’unité.
Corrigé
b) Calculer en cm la longeur de GC. Arrondir le résultat à l’unité.
Corrigé
3. Calculer en cm2 l’aire des trois triangles ABE, CDO et BCG.
Corrigé
4. Calculer en cm2 l’aire du rectangle EBGO.
Corrigé
5. Calculer en cm2 l’aire de la voile.
Corrigé
6. Exprimer l’aire de la voile en m2
Corrigé
Partie 2 : Calcul de la force exercée par le vent
La force exercée par le vent est donnée par la relation : F = p x S où F est la valeur de la force en newton (N), S est la surface de la voile en mètre carré (m2) et p la pression en pascal (Pa).
Calculer la valeur de la force F, agissant sur la voile lorsque le vent atteint la vitesse de 100 km/h, c’est-à-dire que p = 500 Pa. Arrondir le résultat à l’unité.
Corrigé


