Corrigé exercice 5 brevet de maths 2017 sujet 0
Pour régler les feux de croisement d’une automobile, on la place face à un mur vertical. Le phare, identifié au point P, émet un faisceau lumineux dirigé vers le sol.
On relève les mesures suivantes :
PA = 0,7 m, AC = QP = 5 m et CK = 0,61 m.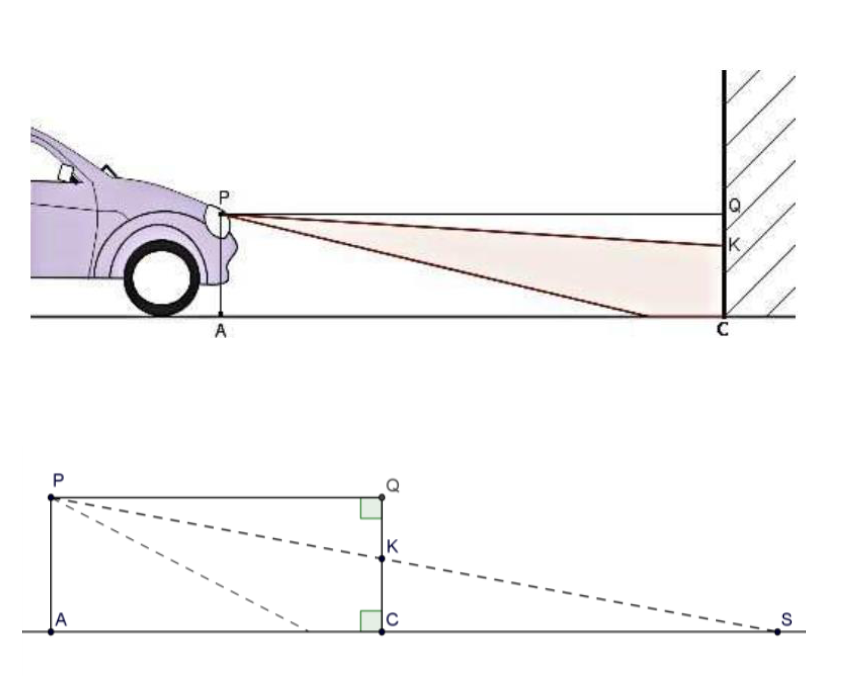
Sur le schéma ci-contre, qui n’est pas à l’échelle, le point S représente l’endroit où le rayon supérieur du faisceau rencontrerait le sol en l’absence du mur.
On relève les mesures suivantes :
PA = 0,7 m, AC = QP = 5 m et CK = 0,61 m.
Sur le schéma ci-contre, qui n’est pas à l’échelle, le point S représente l’endroit où le rayon supérieur du faisceau rencontrerait le sol en l’absence du mur.
On considère que les feux de croisement sont bien réglés si le rapport QK/QP est compris entre 0,015 et 0,02.
1) Vérifier que les feux de croisement de la voiture sont bien réglés.
On remarque que PA = 0,7 m de ce fait QC = 0,7 m
Pour trouver la longueur QK il suffit de faire QK = QC – KC = 0,7 – 0,61 = 0,09 m
Donc QK/QP = 0,09/5 = 0,018
Donc les feux de croisement de la voiture sont bien réglés car 0,015 < 0,018 < 0,02
2) À quelle distance maximale de la voiture un obstacle se trouvant sur la route est-il éclairé par les feux de croisement ?
Les points S, K, C et S, C, A sont alignés dans cet ordre. Et les droites (CK) et (AP) sont parallèles. Donc d’après le théorème de Thalès on a :
Voir le cours en vidéo sur le théorème de Thalès
Partagez
Vous serez aussi intéressés par:
Corrigé exercice 3 brevet de maths 2017 sujet 0- Corrigé exercice 7 brevet de maths 2017 sujet 0
- Corrigé exercice 2 brevet de maths 2017 sujet 0
- Corrigé exercice 4 brevet de maths 2017 sujet 0
- Corrigé exercice 1 brevet de maths 2017 sujet 0
- Corrigé exercice 6 brevet de maths 2017 sujet 0