Fiche de révision Diviseur commun à deux entiers PGCD
I – Définition et méthode
PGCD : Le PGCD de deux nombres entiers naturels, est le plus grand diviseur
commun de ces deux nombres.
Il y a 3 méthodes utilisées pour trouver ce dernier.
Méthode 1: Les diviseurs
1. Etablir la liste des diviseurs des deux nombres
2. On repère tous les diviseurs communs
3. On trouve le plus grand diviseur commun qui est le PDCD de ces deux nombres.
Exemple : trouver le PGCD de 48 et 64
- 1. Diviseurs de 48 : 1 ; 48 ; 2 ; 24 ; 3 ; 16 ; 4 ; 12 ; 6 ; 8
(Ici on utilise les produits égaux à 48, et on s’arrête à 6 x 8 car le premier facteur
dépasserait le second)
Diviseurs de 64 : 1 ; 64 ; 2 ; 32 ; 4 ; 16 ; 8
(Ici on utilise les produits égaux à 64, et on s’arrête à 8 x 8 car le premier facteur
dépasserait le second) - 2. Les diviseurs communs : 1 ; 2 ; 4 ; 8 ; 16
- 3. On a donc PGCD(48 ;64) = 16
Méthode 2 : L’algorithme des soustractions successives
1. Faire la différence entre le nombre le plus grand et le nombre le plus petit
2. Puis faire la différence entre les deux nombres les plus petits à chaque fois en faisant de sorte de soustraire le plus petit au plus grand jusqu’au résultat nul.
3. Le PGCD sera le dernier résultat non nul.
Exemple : Trouver le PGCD de 112 et 74
112 – 74 = 84
84 – 48 = 36
48 – 36 = 12
36 – 12 = 24
24 – 12 = 12
12 – 12 = 0
Le dernier résultat non nul est 12
Donc PGCD(74 ;112) = 12
Méthode 3 : L’algorithme d’Euclide
1. On effectue la division euclidienne du plus grand nombre par le plus petit
2. Puis on refait une division euclidienne avec le diviseur et le reste jusqu’à obtenir un reste nul
3. Le PGCD est le dernier reste non nul
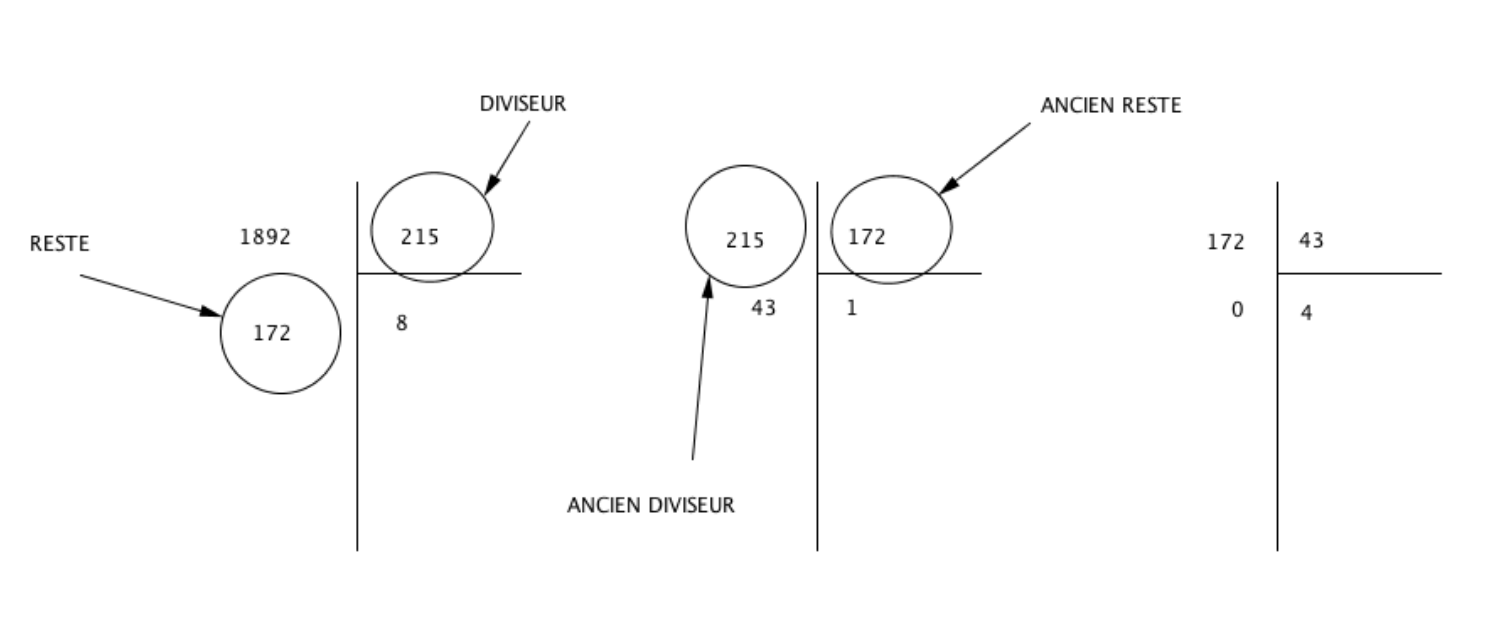
Exemple : Trouver le PGCD de 215 et 1892
Ici on remarque que le dernier reste non nul est 43, donc PGCD (215 ; 1892) = 43
II – Nombres premiers entre eux.
Définition : Si le PGCD de deux nombres entiers naturels est égal à 1, alors ces deux nombres sont premiers entre eux.
Exemple : PGCD (1223 ; 717) = 1
Alors 1223 et 717 sont premiers entre eux.