Fiche de révision Fonctions linéaires
I) Définition d’une fonction linéaire
f (x) = ax .
a est un nombre réel appelé le coefficient directeur de la fonction f .
II) Caractéristiques
- La représentation graphique d’une fonction linéaire est une droite d’équation
y = ax - Cette droite passe par le point de coordonnées (0 ; 0)
- Les images et les antécédents sont proportionnels
III) Méthodologie : Trouver le coefficient directeur d’une fonction linéaire à l’aide d’un point différent de l’origine
Soit le point A(4 ; 6) appartenant à la droite représentative de la fonction f , donner l’expression de la fonction linéaire f .
|
Méthode On sait que f est une fonction linéaire, |
Exemple Ici on va remplacer x par 4, et f(x) par 6 qui sont les coordonnées du point A qui appartient à la courbe de f. f (x) = ax 6 = a * 4 a = 6/4 a = 3/2 On en conclut que f (x) = 3/2 x |
VI Méthodologie – Tracer la droite représentative d’une fonction linéaire
|
Méthode Pour tracer une droite il suffit de connaître |
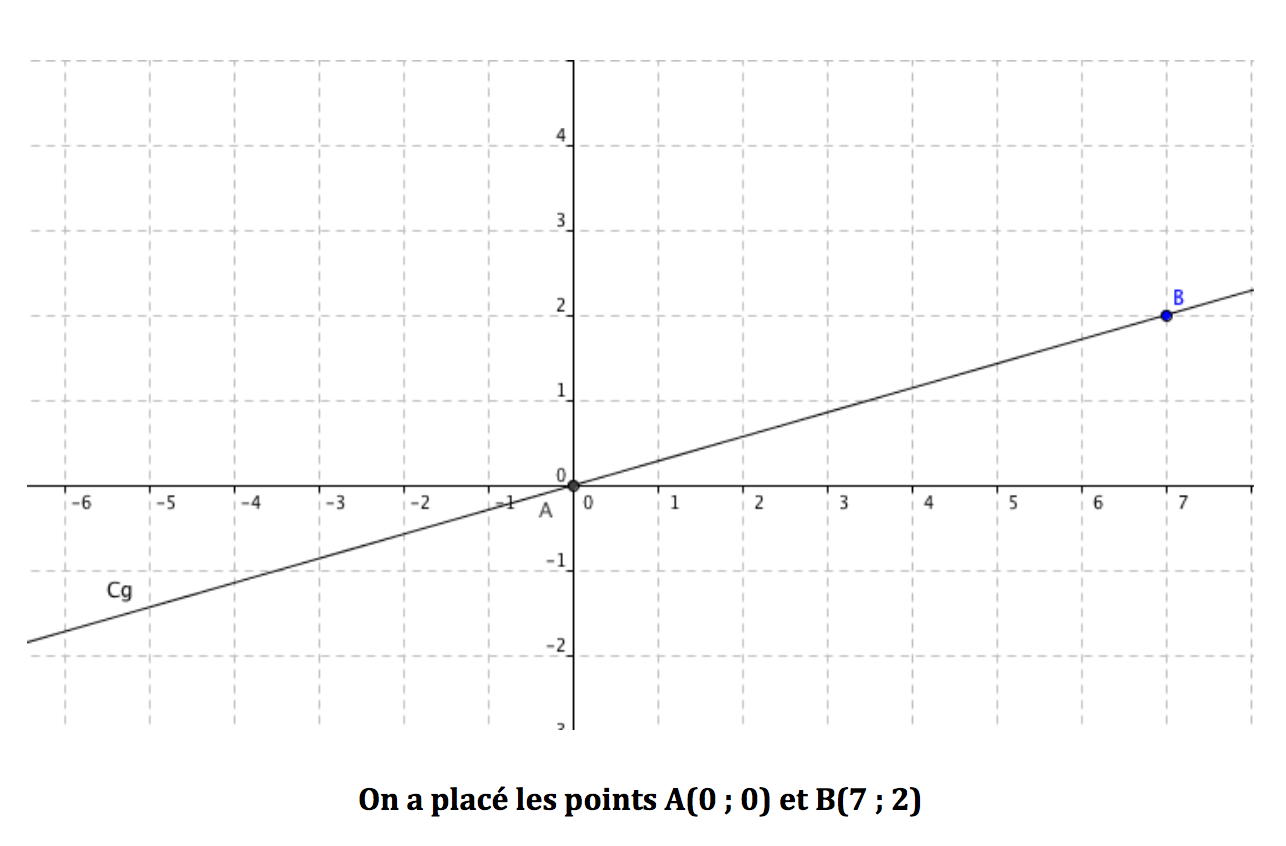
Exemple Soit g(x) = 2/7 x Donc la droite passe par l’origine et par le point de coordonnées (7 ; 2) |
V Méthodologie – Interpréter et trouver le coefficient directeur à l’aide du graphique
La méthode est simple il suffit de prendre deux points et de diviser les variations des
images par les variations des antécédents.
Exemple
Soit la représentation graphique de la fonction linéaire g.
Ici on a donc g(x) = 1/2 x
Remarques
- Il aurait été possible de relever les coordonnées des points et de faire la même
méthode que l’encadré précédent. - Pour la lecture graphique il suffit de faire comme n’importe quelle fonction.