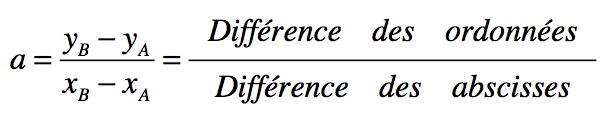Fiche de révision maths fonctions affines
I – Définition d’une fonction affine
Une fonction affine f est une fonction qui à tout nombre x associe un nombre f (x) = ax + b .
a est un nombre réel appelé le coefficient directeur de la fonction f,
b est un nombre réel appelé ordonnée à l’origine.
II – Caractéristiques d’une fonction affine
- La représentation graphique d’une fonction affine est une droite d’équation y = ax + b
- Cette droite passe par le point de coordonnées (0 ;b)
- Les accroissement de y sont proportionnels aux accroissements de x.
III – Méthodologie : trouver le coefficient directeur à l’aide de deux points.
Soient les points A(1 ; 5) et B(3 ; 11) appartenant à la droite représentative de la fonction f , donner l’expression de la fonction affine f .
|
Méthode f est une fonction affine, f (x) = ax + b La formule du coefficient directeur est Pour trouver b, il suffit de remplacer x par l’abcisse d’un des deux points
|
Exemple On applique la formule a = (11 – 5) / (3 – 1) = 6 / 2 = 3 Donc pour le moment il nous manque l’ordonnée à l’origine et nous avons f (x) = 3x + b On utilise ici le point A 5 = 3×1+ b b = 2 On obtient f (x) = 3x + 2 |
voir un autre exemple en vidéo
IV – Méthodologie : tracer la droite représentative d’une fonction affine.
|
Méthode Ici métode presque similaire à celle des fonctions linéaires, il suffit de trouver deux points pour tracer la droite. Il est déjà très simple de prendre le point de coordonnées (0 ; b) On remplace x par une valeur choisie aléatoirement et on relie les deux points pour obtenir la droite demandée.
|
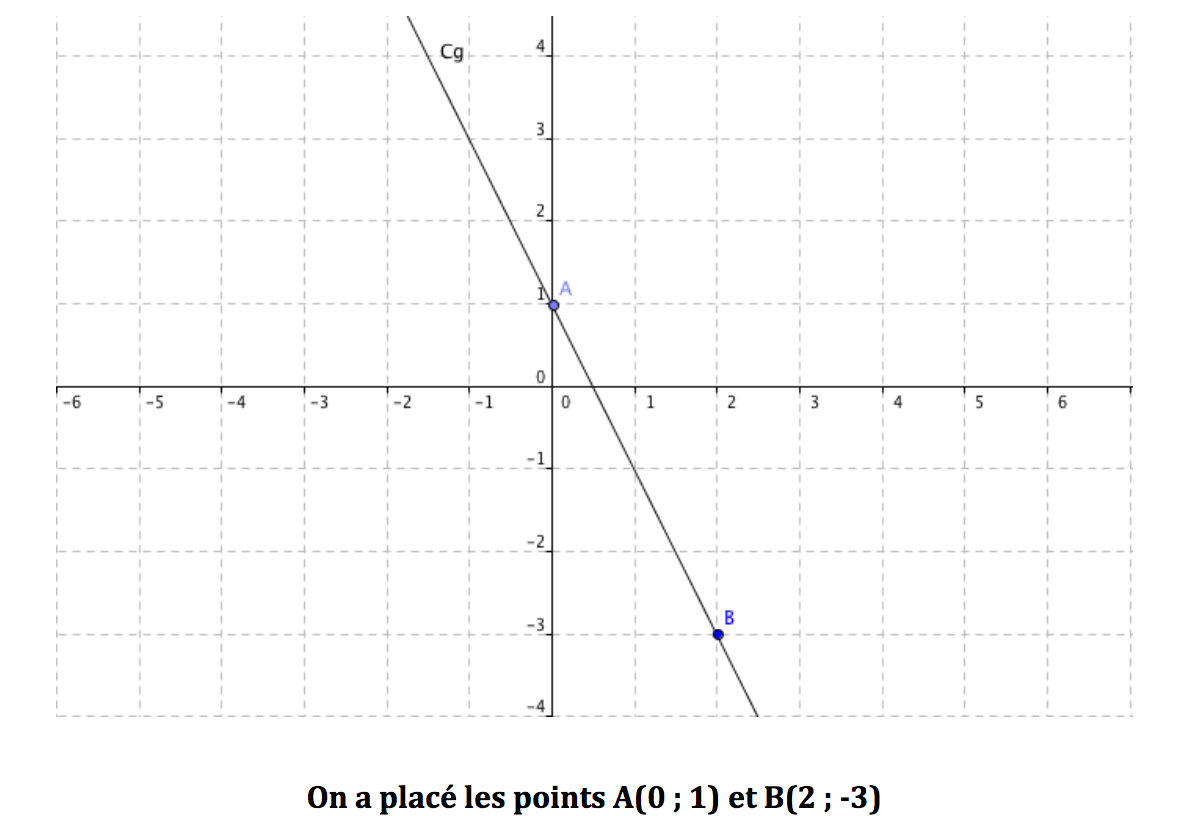
Exemple Soit g(x) = – 2x +1 Prenons x = 2 (ici 2 est choisi au hasard). g(2) = – 2 x 2 + 1 = – 3 Donc la droite passe par les points de coordonnées A(0 ; 1) et B(2 ; -3) (cf graphique) |
voir un autre exemple en vidéo
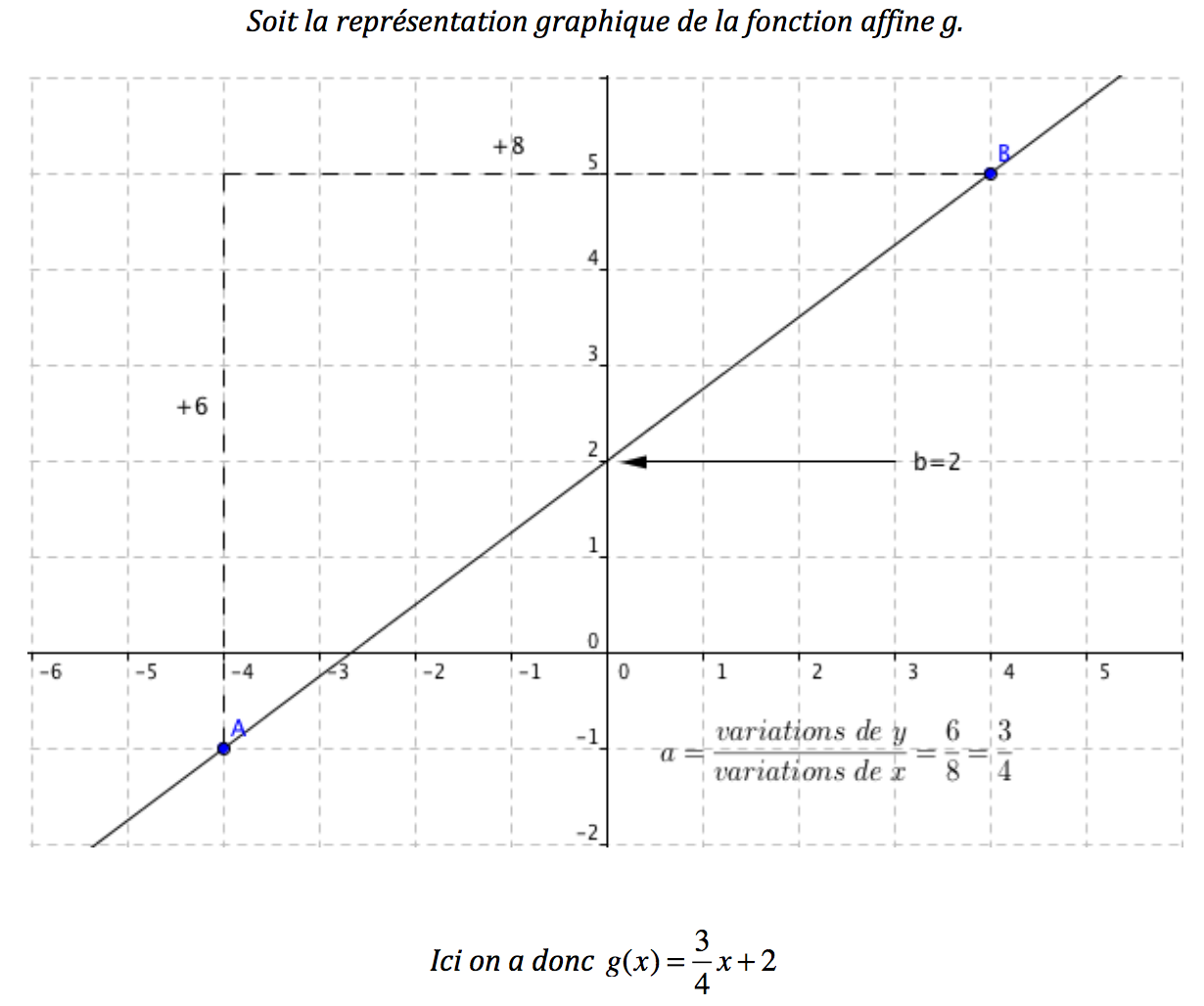
V – Interpréter et trouver le coefficient directeur et l’ordonnée à l’orignie à l’aide du graphique
Pour le coefficient directeur, même méthode que pour les fonctions libnéaires et pour trouver l’ordonnée à l’origine, il suffit de lire l’ordonnée du point d’intersection entre la droite et l’axe de ordonnées.
Remarques :
- Il aurait été possible de relever les coordonnées des points et de faire la même méthode que dans l’envadré précédent.
- Pour la lecture graphique il suffit de faire comme pour n’importe quelle fonction.